O Teorema de Pitágoras

O Teorema de Pitágoras é um dos conceitos mais fundamentais e conhecidos da geometria euclidiana, relacionando os lados de um triângulo retângulo. Ele é atribuído ao matemático grego Pitágoras de Samos, embora evidências históricas sugiram que o conceito já era conhecido por civilizações antigas, como os babilônios e os egípcios, muito antes dele.

O que é um Triângulo Retângulo?

Antes de tudo, é crucial entender o que é um triângulo retângulo. É um tipo de triângulo que possui um ângulo interno de 90 graus (um ângulo reto). Os lados de um triângulo retângulo recebem nomes específicos:
* Hipotenusa: É o lado oposto ao ângulo reto e é sempre o lado mais longo do triângulo.
* Catetos: São os outros dois lados do triângulo que formam o ângulo reto.

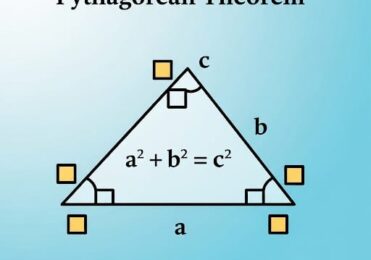
Enunciado do Teorema de Pitágoras

O teorema afirma que:
“Em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.”
Fórmula do Teorema de Pitágoras
Matematicamente, se chamarmos a hipotenusa de c e os catetos de a e b, a fórmula é expressa como:
a^2 + b^2 = c^2
Como o Teorema é Aplicado
O Teorema de Pitágoras é amplamente utilizado para encontrar a medida de um dos lados de um triângulo retângulo quando as medidas dos outros dois lados são conhecidas.
Exemplo:
Imagine um triângulo retângulo onde um cateto mede 3 cm e o outro cateto mede 4 cm. Para encontrar o comprimento da hipotenusa, aplicamos o teorema:
a = 3 cm
b = 4 cm
c = ?
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2
c = \sqrt{25}
c = 5 cm
Portanto, a hipotenusa mede 5 cm. (Este é um exemplo de um “terno pitagórico” muito conhecido: 3, 4, 5).
Demonstração (Ideia Geométrica)
Uma das maneiras intuitivas de “ver” o Teorema de Pitágoras é através de uma demonstração geométrica. Imagine quadrados construídos sobre cada um dos lados de um triângulo retângulo. O teorema afirma que a área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os catetos.

Significado e Aplicações

O Teorema de Pitágoras é de extrema importância não apenas na matemática, mas também em diversas áreas do conhecimento e do cotidiano:
* Geometria: É a base para muitos outros teoremas e conceitos geométricos.
* Engenharia e Arquitetura: Usado no cálculo de distâncias, na construção de estruturas, no planejamento de telhados, rampas e na determinação da diagonal de objetos.
* Física: Aplicado em cálculos de vetores, trajetórias e forças.
* Navegação e Cartografia: Utilizado para calcular distâncias entre pontos em mapas e no planejamento de rotas.
* Computação Gráfica: Essencial para cálculos de distâncias, projeções e modelagem 3D.
* Cotidiano: Ajuda a resolver problemas práticos como determinar o tamanho de uma escada necessária para alcançar uma altura específica ou a distância entre dois pontos em um terreno.

Em resumo, o Teorema de Pitágoras é uma ferramenta poderosa e universal que relaciona de forma elegante a geometria e a álgebra, com aplicações que transcendem a sala de aula, sendo fundamental para o desenvolvimento de diversas tecnologias e construções.